图论(Graph Theory)其三・欧拉回路(Euler Tour)与图遍历(Graph Traversal)
前言
尽管有些颠倒,在介绍完一些图当中的基本定义之后,让我们跟随欧拉的脚步,来看看图论这个领域上的第一个被提出的问题 — 柯尼斯堡七桥问题。
1.欧拉回路
据传在东普鲁士柯尼斯堡(今日俄罗斯加里宁格勒)市区跨普列戈利亚河两岸,河中心有两个小岛,在岛屿之间一共建设了七座桥梁,如下图所示。
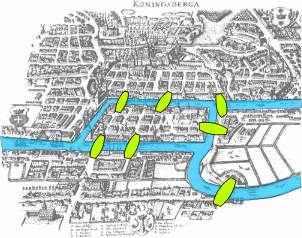
那么有没有可能在所有桥都只经过一次的情况下,走遍这七座桥呢?—这个问题在如今被称作是柯尼斯堡七桥问题。欧拉在1736年于圣彼得堡科学院发表的论文中将这个问题抽象为平面上点与边的组合,将每个区域视为一个顶点,而将桥视为连接两个顶点(区域)的边,如下图所示。
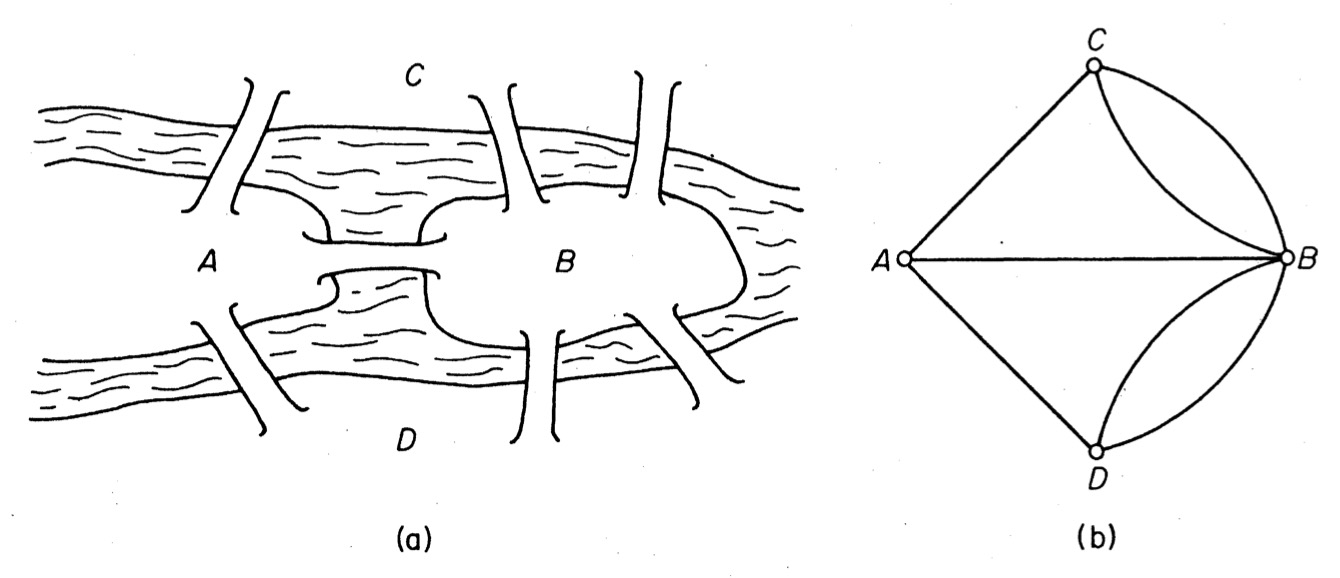
这样一来,问题就变成了
对于上述给定的有着四个顶点和七条边的连通图$G(V, E)$,是否存在一条通过所有边有且仅有一次的回路?
在此基础之上,欧拉提出了一个更加一般化的的问题
对于任意给定的图$G(V, E)$,如何判断图中是否存在一条通过所有边有且仅有一次的回路?
这个抽象之后的问题也被称为图上的一笔画问题,这条经过所有边有且仅有一次的回路,也被称作欧拉回路(Euler Tour),基于此,一条经过所有边有且仅有一次的路径也被称作欧拉路径(Euler Path)。
那么这个问题如何解决呢?欧拉在他的论文中指出,
连通无向图$G=(V, E)$存在一条欧拉路径当且仅当$G$中度数为奇数的顶点个数为$0$或者$2$。
连通无向图$G=(V, E)$存在一条欧拉回路当且仅当$G$中度数为奇数的顶点个数为$0$。
定理的证明并不难,假设图$G$中存在一条欧拉回路,基于回路的定义,对于图中任一顶点来说,若欧拉回路中有一条边进入该点,则必须有一条边从该点流出,因此欧拉回路中任意一点的度数均为偶数,也即图$G$中所有点的度数均为偶数。倘若图$G$中存在一条欧拉路径,同理可知,仅有起点和终点的度数为奇数。
反过来,如果图中没有度数为奇数的顶点,这意味着每个点至少与两条边相连。那么我们可以随便从一个点出发,途径某些顶点最终回到起始点,构成一个圈。如果这个圈就是一条欧拉回路,那么万事休矣。若非如此,我们可以将该圈上的边从图中删去,由于圈上每个点的度数为2,这意味着删去之后的图所有顶点的度数仍为偶数,于是我们重复这个寻找圈的过程,如下图所示。
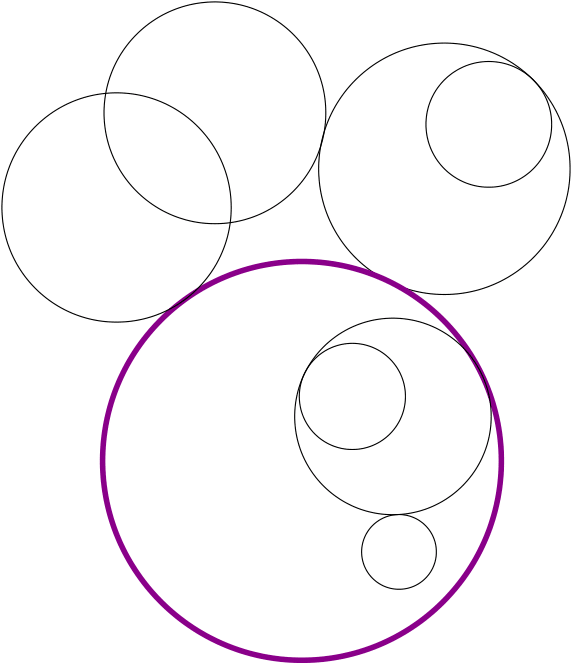
两个相互连接的圈实际上可以看做是一个更大的圈,因而这些圈组合起来,便是一条欧拉回路了。若是图中有两个奇数度数的顶点$u, v$,我们可以在一开始额外加入一条边$uv$。在最终得到欧拉回路之后将其删去,也就得到了一条起点与终点分别为$u$与$v$的欧拉路径。 $\square$
存在欧拉回路的图通常会被称为欧拉图。 尽管欧拉回路可以通过从任意一点出发遍历所有边回到起点而构成,就像我们画一笔画那样,但并非所有的路径都可以拓展成为一条欧拉路径(所谓拓展,指的是在已有的路径终点逐条增添新的边,使其构成一条更长的路径或圈),Øystein Ore指出
令$G=(V,E)$为一个至少具有$3$个顶点的欧拉图,$v \in V$为$G$中的一个顶点。以$v$为起点的每一条路径都可以拓展为一条欧拉回路当且仅当从$G$中删除点$v$及其相邻接的边之后的图(通常以$G - v$表示)是一个森林。
$\Rightarrow$,假设$G - v$并非森林,这意味着其中至少包含一个圈$C$。由于$G$是欧拉图,从中删去一个圈并不影响点度数的奇偶性,因此图$G - E(C)$仍然是欧拉图。这意味着$G - E(C)$中也存在一条欧拉回路$P$。 由于$C \subseteq G - v$,其中不包含点$v$,因此有$v \in V(P)$。我们可以将该欧拉回路看做是一条以$v$为起点的路径,由于与$v$邻接的所有边都已经存在于$P$中,很显然,这条路径是无法拓展为原图$G$的欧拉回路的,矛盾。
$\Leftarrow$,令$P$为以$v$为起点的一条路径,我们对其进行最大程度的拓展,得到路径$P’$。 考虑到$G$当中的顶点度数均为偶数,路径若是进入某个顶点,就必然能从该顶点走出去,因此路径$P’$将会是一条包含了点$v$的回路,且其中会包含所有与点$v$邻接的边。 我们从$G$中删去路径$P’$,由于$P’$是一条回路,$G - E(P’)$仍然是欧拉图。 因此,除非路径$P’$已经包含了$G$中所有的边,否则$G - E(P’) \subseteq G - v$不可能是森林—其中会存在一条欧拉回路。 $\square$
2.图遍历
所以,我们该如何从一张给定的图中寻找并输出一条欧拉回路(路径)呢。在回答此问题之前,我们得先从如何搜索一条普通路径,或者,如何从一个点出发,依次访问其所在连通分量的其他点。这也被称之为图的遍历。
图遍历的思想其实是非常简单的,我们需要的仅仅是通过某种规定的顺序,避免访问到重复的顶点(或边),以及准备好走投无路时的解决方案即可。最常被使用的两种搜索方式分别叫做深度优先搜索(Depth First Search,DFS)与广度优先搜索(Breadth First Search,BFS)。
深度优先搜索的想法非常简单,在选择下一个将要访问的顶点(或边)的时候,总是选择当前所在顶点的一个尚未被访问过的邻居(或邻边)并前往这个邻居,以相同的方法进行下一个点的选择。若当前所在顶点已经不存在这样的选择,则退回上一个访问的顶点,写成伪代码的话,即
Input: Undirected graph G=(V,E) and a specific vertex u
Output: Vertices of V in DFS order
Algorithm DFS(G, u)
label vertex u as visited
for each neighbor v of u do
if v is not visited then
DFS(G, v)
也就是说,每到达一个新的点,便将该点作为新的起点进行接下来的探索。尽管不那么准确,这种邻居的邻居的邻居的邻居的探索方式,总的来说是一直在向着远离起点的方向进行,向着未知的深处进行,因此我们叫它深度优先搜索。
与之相对的,广度优先搜索的核心是由近到远,按距离进行搜索。当然,按距离这个说法听起来听唬人, 我们将到起始点距离为$i$的顶点称之为第$i$层的顶点,则第$0$层即为我们探索的起始点。
倘若探索确确实实按着距离进行的话,那么当访问完第$i$层时,所有距离起始点小于$i$的顶点都已经被访问了。 那么第$i+1$层呢,这些顶点距离起始点的距离为$i+1$,与第$i$的距离差只有$1$,也就是一条边, 因此,他们与第$i$的顶点应该是邻居关系,这样我们才能够以一条边的代价(距离1的代价)从第$i$层抵达第$i+1$层。这意味着,第$i+1$的顶点实际上是第$i$层的,尚未被访问过的邻居。
基于上面的思考,我们可以给出广度优先搜索的伪代码了。
Input: Undirected graph G=(V,E) and a specific vertex u
Output: Vertices of V in BFS order
Algorithm BFS(G, u)
current_set = {u}
next_set = {}
while current_set is not empty do
for each vertex v in current_set do
for each neighbor w of v do
if w is not visited then
label vertex w as visited
next_set.append(w)
current_set = next_set
next_set = {}
其中current_set即为我们当前正在访问的,到起始点距离为$i$的顶点,而current_set中的顶点的尚未被访问过的邻居,将被置于next_set中,供下一轮探索。
除了使用两个集合分别存储第$i$层与第$i+1$需要访问的顶点之外,也可以使用一个先进先出的队列来解决顶点访问顺序的问题—不过这就不属于图论范畴了。
至此,我们便掌握了如何从给顶点出发沿着邻边访问其他点的方法—而这也正是寻找两点之间路径的方法。
3.回到欧拉回路
有了图遍历的支撑,我们可以开始试着基于上述的两种探索方式,去图中寻找一条欧拉回路了—欧拉回路本质上也是一条路径,而这正是图遍历算法所干的事情。
基于我们在第一节最后所作的证明—不断的从图中寻找回路进行拼接—我们可以得到如下从任意给定给的图中寻找欧拉回路的算法
Input: Undirected graph G=(V,E), no or exactly two nodes have odd degree
Output: List of nodes in Eulerian cycle
Algorithm Hierholzer(G)
if G is not eulerian then return
take an arbitrary vertex u from V
T = {} // an empty tour
while there exists an edge in G
take a vertex v with unvisited edge from T
find a cycle C which start from v
integrate C in T
delete all edges in C
该算法于1873年被Hierholzer提出,其复杂度为$\mathcal{O}(\lvert E \rvert)$。
除此之外,我们也可以使用被称作Fleury算法进行欧拉回路的构建,其从一度数为奇数的点(若不存在这样的点,则从任意一点)出发,在每次选择边加入路径时,除非没有其他边可选,否则不选择桥(切边)。
在已知哪些边是切边的情况下,上述过程只不过是一个有限定条件的图搜索(遍历)。因此问题的核心转变为如何确定图中哪些边是切边。
一个最简单的方案则是通过删除每一条边之后,判断图是否连通的方式来确定哪些边是切边—判断连通性是非常简单的,我们只需要从任意一点出发做一个深度优先或广度优先搜索,看看能不能访问到其他所有的点即可。
由于搜索的复杂度取决于有多少条边需要访问,因此通过这种方式判断一条边是否为切边的复杂度为$\mathcal{O}(\lvert E \rvert)$。 因而,获取所有切边的复杂度来到$\mathcal{O}(\lvert E \rvert ^2)$。这就要比上面的Hierholzer算法慢多了。
4.后记
懒惰是万恶之源。
