图论(Graph Theory)其二・树(Tree)
前言
没有比树更简单的图了。
1. 从树的定义出发
对于无向图$G = (V, E)$,若其无圈且连通,则我们称其为树,若其无圈不连通,则称之为森林(Forest)。
由树的定义可以直接得到两条简单而又非常重要的性质
树中任意两点之间的路径是唯一的。 $\lvert V \rvert = \lvert E \rvert -1$
对于第一条,若两点之间存在两条不同的路径,那么这两条路径可以构建成圈; 而第二条可以藉由数学归纳法进行证明,每新增一条边,由于不能够形成圈,因此新增边不能连接图中已有的两个顶点,而必须连接一新一旧。
由于树中任意两点之间的路径唯一,这意味着移除任何一条树边都将使得树不连通,即任何一条树边都是一条切边。 同理,树中任何一个点都是切点。
由顶点的度的定义可知,$\sum_{v \in V} d(v) = 2 \lvert E \rvert$。 因此对于树而言,有
\[\sum_{v \in V} d(v) = 2 \lvert E \rvert = 2 \lvert V \rvert - 2\]考虑到对于树种任意一点$v$,有$d(v) \ge 1$,因此我们可以知道,任意的树至少具有两个度数为$1$的顶点。 我们将树中度数为$1$的顶点称之为叶(Leaf)。
在许多时候,我们将树中的某个节点视作根(Root),从有向图的角度去看待一棵树—以一个形象的比喻,若将树视为族谱,那么根节点即为我们的祖先,而所有边的方向均由前辈指向后辈。 有根树中任意两点$u, v$的距离可以藉由二者到根的距离算出,
\[\text{dist}(u, v) = \text{dist}(r, u) + \text{dist}(r, v) - \text{dist}(r, w)\]其中$r$为树根,而$w$为点$u$与$v$的最小公共祖先(Least Common Ancestor)。
2. 生成树
无向连通图$G = (V, E)$的生成树(Spanning Tree)$T = (V, E_T) \subseteq G$是$G$的一种特殊子图,其为一棵树且拥有和$G$相同的点集。
生成树可以从某种意义上看做是图$G$的骨架,在之前的图描画与整数规划・交叉数扮演着重要的角色。
对于图而言,它的骨架可以有很多个,因此我们接下来要解决的问题便是,对于任意给定的连通无向图$G = (V, E)$,我们能否计算出其不同生成树的个数。 这里我们可以认为每个点有他唯一的标识(Label)或者说名称($v_1, v_2, \ldots$),我们说两棵树是相同的当且仅当其每一个点每条边的标识都相同。
幸运的是,德国物理学家基尔霍夫已经帮我们解决了这个问题,他在其著名的Matrix-Tree定理中指出,
对于给定的连通无向图$G$,其不同生成树的个数为$\text{det}(L^G_{[i]})$,$i$为区间$[1, \lvert V \rvert]$中的任意整数。
这里$L^G$为$G = (V = {v_1, v_2, \ldots, v_n}, E)$的拉普拉斯矩阵,其定义如下:
\[L^G_{i,j} = \left\{ \begin{array}{ll} d(v_i) & \text{if $i = j$} \\ -1 & \text{if $i \neq j$ and $(v_i, v_j) \in E$} \\ 0 & \text{otherwise} \end{array} \right.\]而$L^G_{[i]}$表示从$L^G$中移除了其第$i$行第$i$列的矩阵。
在证明这个定理之前,我们需要一点点准备工作。
令$A$为一个$n$行$n$列的矩阵,$E_{ii}$为仅在位置$(i, i)$为$1$,其余地方均为$0$的矩阵。则有 $\text{det}(A + E_{ii}) = \text{det}(A) + \text{det}(A_{[i]})$
我们可以直接从行列式的定义出发来证明,注意到
\[\text{det}(A=(a_{ij})) = \sum_{\pi} \text{sgn}(\pi) a_{1\pi(1)} a_{2\pi(2)} \cdots a_{n\pi(n)}\]由于我们将$a_{ii}$变为了$a_{ii} + 1$,因此除开$a_{ii}$之外的行列都需要与这里的$+1$相乘,得到一个除开$a_{ii}$之外的全排列和式,也即$\text{det}(A_{[i]})$。
做好准备工作之后,让我们正式进入Matrix-Tree定理的证明。
若图$G$是一个只有两个顶点的空图,则我们有
\[L^G = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}\]因此有$L^G_{[i]} = [0]$,即有$\text{det}(L^G_{[i]}) = 0$。
我们用$\tau(G)$表示图$G$中生成树的个数,并在图上定义一种叫做边收缩(Edge Contraction)的操作,即将某条边两端的点融合。 对于任意的边$e=uv \in E$,图$G$的边收缩图$G / e$的构造方式如下,我们从$G$中删去$u,v$两点,加入一个新的点$w$,并将$w$与$u, v$的邻居进行连接。倘若某个点$p$既是点$u$的邻居,也是点$v$的邻居,那么在收缩图中,将有两条$wp$边。
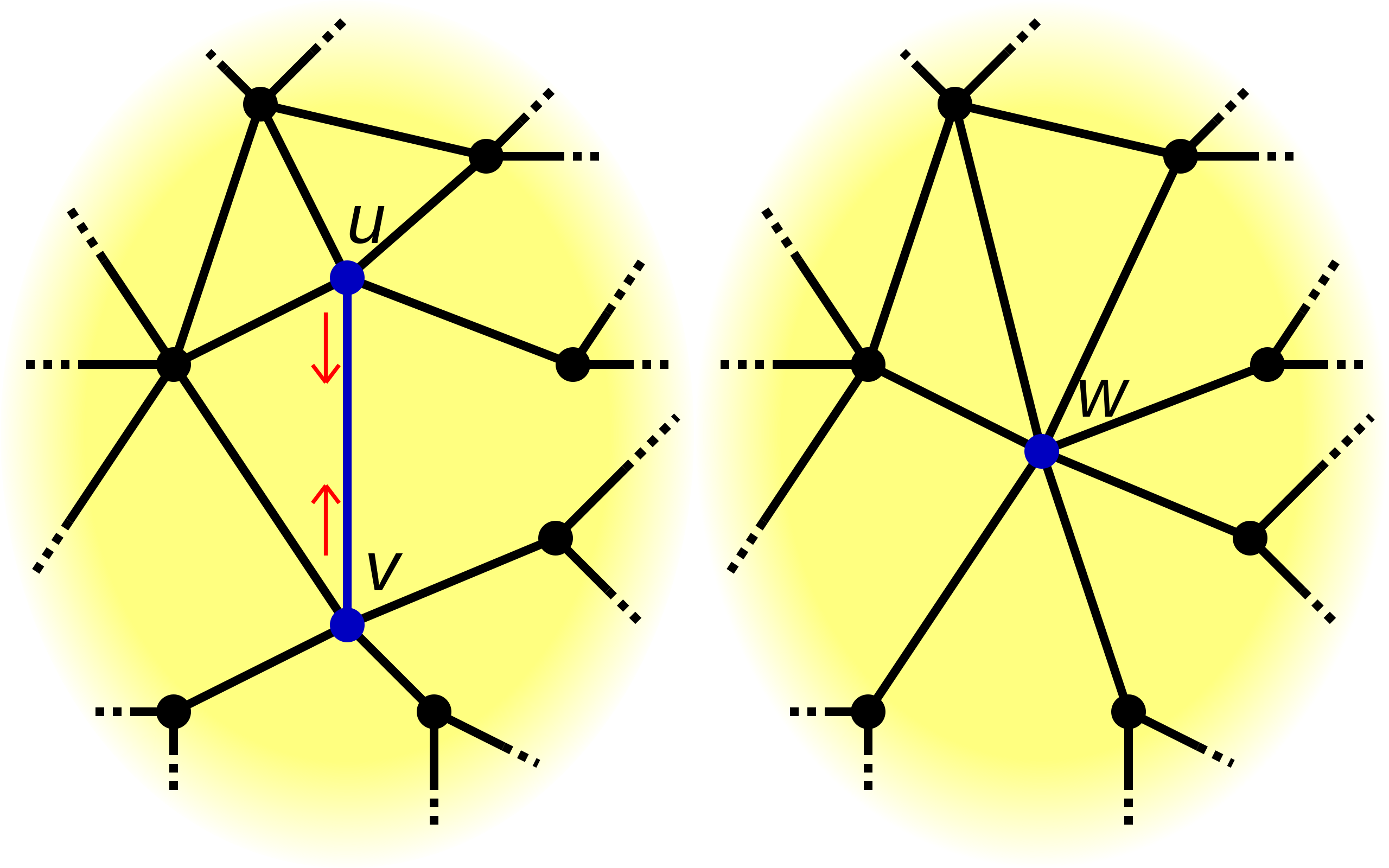
对于图$G$中的某点$v_i$,由于$G$是连通图,因此存在一条邻接点$v_i$的边$e = (v_i, v_j)$。 如果我们要求生成树一定包含$e$,那么这类生成树可以看做是在收缩图$G / e$上寻找的生成树,因此一共有$\tau(G / e)$个。 而如果我们要求生成树一定不含$e$,那么这类生成树可以看做是在子图$G - e$上寻找的生成树,因此一共有$\tau(G - e)$。
因此有
\[\tau(G) = \tau(G / e) + \tau(G - e)\]顺着这个想法,我们来看看他们所对应的拉普拉斯矩阵有什么联系。 注意到如果我们移除了边$e = (v_i, v_j)$,点$v_i, v_j$的度数会减一,因此有
\[L^{G}_{[i]} = L^{G - e}_{[i]} + E_{jj}\]根据我们之前的准备工作可以得到
\[\begin{align} \text{det}(L^G_{[i]}) &= \text{det}(L^{G - e}_{[i]} + E_{jj}) \\ &= \text{det}(L^{G - e}_{[i]}) + \text{det}(L^{G - e}_{[i, j]}) \\ &= \text{det}(L^{G - e}_{[i]}) + \text{det}(L^{G}_{[i, j]}) \end{align}\]因为一旦我们移除了拉普拉斯矩阵的$i$行$i$列与$j$行$j$列,矩阵中已经没有与$v_i, v_j$相关的元素。
至于$L^{G/e}$,我们可以将边收缩视作为将点$v_i$合并到了$v_j$上去,因此我们认为$L^{G/e}$并没有与点$v_i$相关的行与列。 因而有
\[L^{G/e}_{[i]} = L^{G}_{[i]}\]基于这个,我们有
\[\begin{align} \text{det}(L^G_{[i]}) &= \text{det}(L^{G - e}_{[i]}) + \text{det}(L^{G/e}_{[j]}) \\ &= \tau(G - e) + \tau(G / e) \\ &= \tau(G) \end{align}\]命题得证。
若图$G$为完全图,此时有
\[L^G = \begin{pmatrix} n-1 & \cdots & -1 \\ \vdots & \ddots & \vdots \\ -1 & \cdots & n-1 \end{pmatrix}\]这里$n = \lvert V \rvert$,不难算出$\text{det}(L^G_{[i]}) = n^{n - 2}$,也即凯莱公式(Cayley’s formula)。
事实上,凯莱公式这一特殊情况可以藉由我们以前提到过的生成函数来证明
令$P_n$为一个$n$个变量的多项式,它的每一项$x^{\alpha_1}_1 x^{\alpha_2}_2 \cdots x^{\alpha_n}_n$的系数 与完全图$K_n = (V = {v_1, v_2, \ldots, v_n}, E)$的生成树数量关联,这里我们将生成树看做是一棵有根树,并且其中点$v_i$拥有$\alpha_i$个孩子。 则有$P_n = (x_1 + x_2 + \cdots + x_n)^{n-1}$。
我们可以用归纳法证明这个定理,当$n=1$时,$P_1 = x^0_1$。一个点,只能作为根节点,且没有孩子。命题成立。
当$n>1$时,我们先不妨设$v_n$是一个叶子,此时$\alpha_n = 0$,由于这片叶子可以长在$n-1$个点所构成的树上的任何一个位置,即附着于任何一个顶点上,此时我们有
\[\begin{align} Q &= P_{n-1} (x_1 + x_2 + \cdots + x_{n-1}) \\ &= (x_1 + x_2 + \cdots + x_{n-1})^{n-1} \end{align}\]这是一个很有趣的结果,它告诉我们若$\alpha_n = 0$,则
\[x^{\alpha_1}_1 x^{\alpha_2}_2 \cdots x^{\alpha_n}_n\]的系数和
\[(x_1 + x_2 + \cdots + x_{n-1})^{n-1}\]是一样的。
而同时我们还知道这样两条事实,第一,若$\alpha_n = 0$,此时$Q$实际上就是$P_n$;其次,$P_n$与$Q$中度为$n-1$的变量
那么若$P_n \neq (x_1 + x_2 + \cdots + x_n)^{n-1}$,我们假定其中存在某项$x^{\alpha_1}_1 x^{\alpha_2}_2 \cdots x^{\alpha_n}_n$不相同。 注意到$P_n$实际上是一个度数为$n-1$齐次对称的多项式,一个点至多有$n-1$和孩子,多项式$(x_1 + x_2 + \cdots + x_n)^{n-1}$亦是如此。
由$\sum_i \alpha_i = n-1$可知,存在一个$\alpha_{i^\star} = 0$的变量$x_i$。 不是一般性,我们假设这里$i^\star = n$。
由$P_n$的对称性可知若存在一项不同,则至少还会存在另一项不同,但上面提到的事实告诉我们,若$\alpha_n = 0$,$P_n = (x_1 + x_2 + \cdots + x_n)^{n-1}$,不应该存在其他不同项,产生了矛盾。
后记
想来距离上一次写图论的复习笔记已经一年过去了,懒散的消磨了一年时光,说来非常惭愧。 树是图论中非常重要和基础的结构,在以后的学习中,我们还会经常遇到并使用它的一些性质。 第二部分中提到的生成树,除开文中提到的计数之外,还有一个在有权图中寻找总权重最小的生成树,被称之为最小生成树的问题,也是图论中非常重要的一个问题。 但考虑到其内容涉及到算法且为一个经典的组合优化问题,在不久的将来我们会单独写一篇相关的内容来进行讲解,这次肯定不会鸽一年这么久了。
