图描画(Graph Drawing)与整数规划(Integer Programming)・交叉数(Crossing Number)
前言
找份活干比想象中要难得多,因此这也算是苦中作乐罢,来讲一个曾经研究过的内容—并非什么非常好的回忆,只记得当时想出来的方案实验结果太差而因此小小的更换了课题。大约是两年前时候,我进行了一段时间的使用整数规划对图描画中的一些问题进行建模的研究,目的是为了借由CPLEX等高速的整数规划求解器来效率的解决一些图描画中的NP困难问题。图描画问题从数学的角度来说是相当困难的一类问题,但从视觉来说,却是很容易想象与理解的,于是本文不会有什么严密的数学内容—苦中作乐,数学太多,可就乐不起来了。
1.图描画问题
我们所讨论的图,指的是集合$V$,通常称之为点集,以及一个描述点与点之间是否存在关联的集合$E \subseteq V \times V$,通常称之为边集,所组成的元组。由于图是离散数学中一个相当基础的概念,因此这里就姑且假定大家都对图的基本概念有一些掌握,而不再加以赘述了。不过值得注意的是,在这里我们只讨论简单无向图,即没有自圈与多重边的无向图。
那么对于一个给定的图,例如我们假设
\[V = \{v_1, v_2, v_3, v_4\}\] \[E = \{v_1v_2, v_1v_3, v_2v_3, v_1v_4, v_2v_3, v_3v_4\}\]也即四个点的完全图$K_4$,我们可以很自然的将其画在平面上(如下图),就像我们平时讨论图论问题的时候一样。
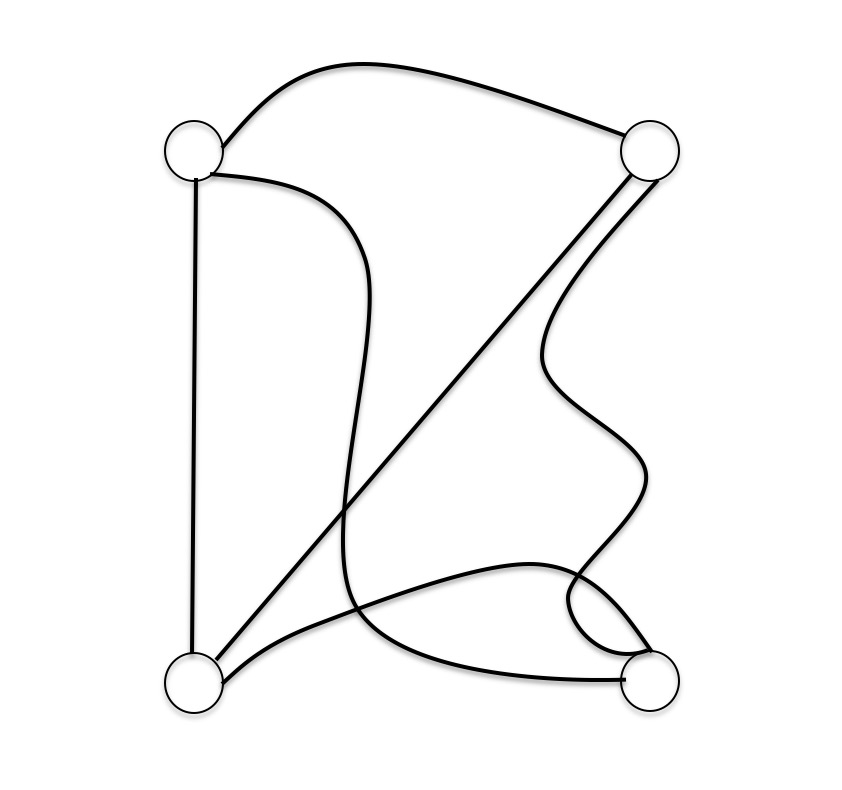
通俗的说,所谓的图描画,便是指上图中我们所做的那样,将一张图绘制在平面上的一种方式—我们将点绘制为圆,将边绘制为弧线,以连接两个不同的点。
从现实的绘制来说,我们所绘制的线是有粗细的,点也是有大小的,但作为一个数学问题,我们不考虑这些,即,我们认为我们所绘制的点是没有大小的,且弧线也是没有宽度的。不仅如此,我们还需要增加几样要求,以便于我们讨论接下来的问题。第一,点与点,点与边以及边与边在绘制的时候不能够发生任何形式的重合;第二,弧线只能为一条简单的弧线,它不应与自己发生交叉;第三,倘若两条边所对应的弧线在绘制的时候发生了交叉,那么他们至多只能有一个交点。你可能会对第二与第三个要求感到好奇,但事实上,自己与自己的交点以及两条不同的边之间多于一个的交点实际上是没有意义的。想象某条边像一堵城墙一样绘制在平面上,那么倘若你要出城,则需要与其交叉,若你不需要出城,则不需要交叉,仅此而已,再多的交叉,也只不过是在这两者之间循环。
因此,我们同样也不在乎你在绘制一条边的时候转了几个弯,画的是否好看。我们只在乎其是否和其他边发生了交叉,因此你可以在某种程度上认为,在描画的时候,我们使用尽可能简单的线条去进行绘制。而我们想要解决的问题也正与描画中的不同弧线之间的交叉点的个数有关—给定一张图,我们希望知道其绘制在平面上时,至少会有多少个交叉点,并且更进一步,我们希望能够得到这种使得交叉点最小的绘制方法。举例来说,四个点的完全图$K_4$可以绘制为如下形式,使得其不存在交叉点,而五个点的完全图$K_5$则不行。
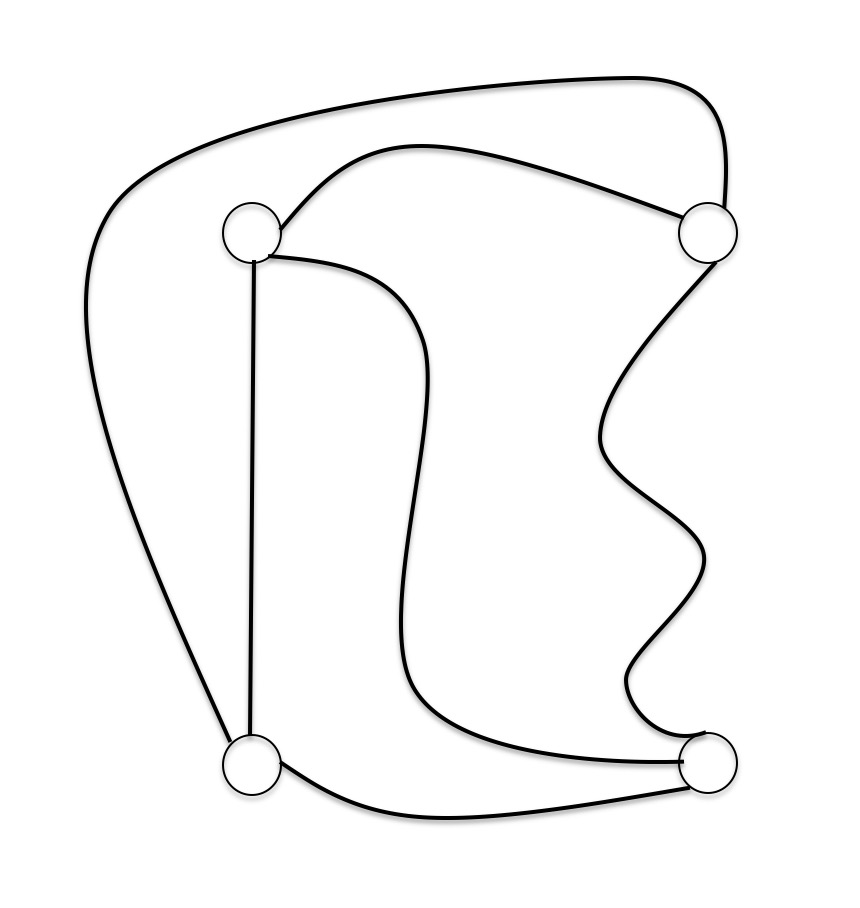
对于图$G$来说,我们将$G$绘制在平面上时所能达到的最小交叉的数量记做$\text{cr}(G)$,称作图$G$的交叉数(Crossing Number)。对于任意给定的图$G$,计算其交叉数是一个NP困难问题,这意味着我们无法快速高效的去求得它,那么想要更进一步得到绘制方法,更是难上加难了。
你可能会问,为什么我们要解决这样一个问题呢?实际上我也不知道,尽管它的确是图描画领域中最基本且重要的问题。 我曾在某些面试的时候被问到同样的问题,然后预想了一些可能的应用场景,或许是在信息可视化中能够有所应用,但是都有些牵强—这个问题的设定还是过于理想化了。
2.整数规划
我们在高中时期都学过一点点线性规划的基本概念,其指的是目标函数与约束条件均为线性的最优化问题。因而一般而言,首先得有一个线性的需要取得最大值的函数,例如
\[f(x_1, x_2) = c_1 x_1 + c_2 x_2\]然后,我们有一系列约束条件,
\[\begin{align} a_{11} x_1 + a_{12} x_2 \le b1 \\ a_{21} x_1 + a_{22} x_2 \le b2 \\ a_{31} x_1 + a_{32} x_2 \le b3 \end{align}\]以及最后,我们可能对变量的取值范围也有一些要求,
\[x_1 \ge 0, x_2 \ge 0\]那么倘若我们要求变量均为整数,即
\[x_1, x_2 \in \mathbb{N}\]则我们称其为整数规划,是线性规划的一种极其特殊的形式,其于一般情况下同样为NP困难问题。而我们今天的主要内容,便是讲述如何将计算图的交叉数并得到对应绘制方法的问题,建模为整数规划问题。直觉上说,两者除了同为NP困难问题之外,看起来几乎是八竿子打不到一块去的两个问题,但我们确有方案能够完成建模。
3.骨架
倘若一条边所对应的弧线能够在平面上任意穿梭,那么别说是求得绘制方法了,单单是描述绘制方法都是相当不容易的。因而我们大工程的第一步,便是想办法去进行限制,或者说为绘制设定一个标准,使得任意一种描画均可以按照我们所设立的标准去进行描述。这里我们首先想到的,便是利用生成树(Spanning Tree),去为我们的图确定一个骨架。
令$G = (V, E)$为我们待描画的图,其中
\[V = \{v_1, v_2, v_3, v_4, v_5\}\] \[E = \{v_1v_2, v_1v_3, v_1v_4, v_2v_4, v_2v_5, v_3v_4, v_4v_5 \}\]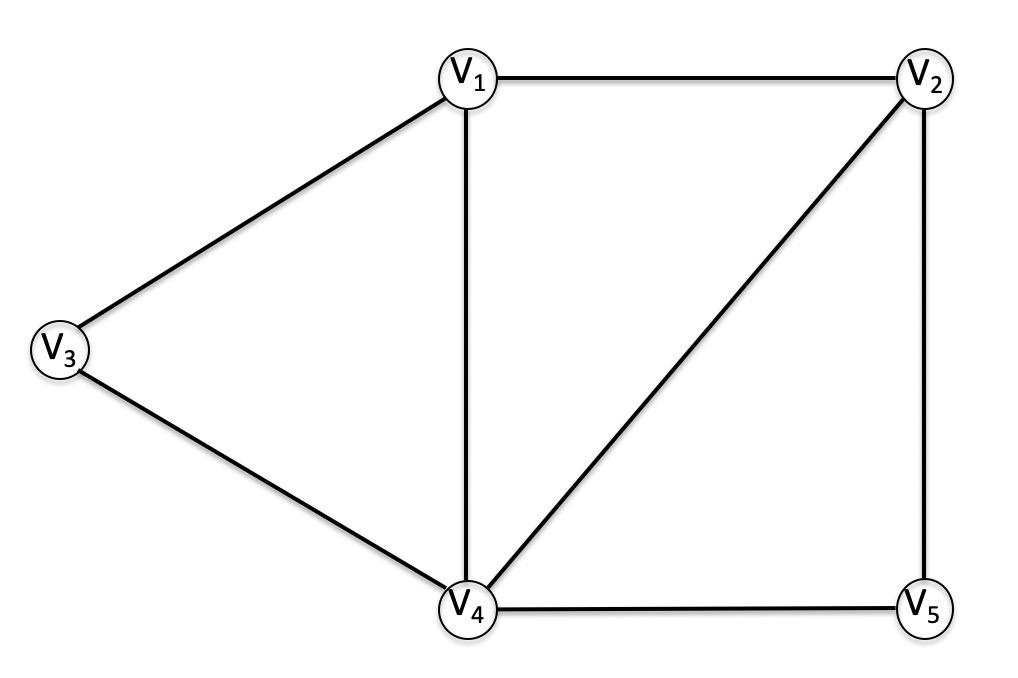
首先,对于每一条边$e = v_i v_j \in E$,我们为其构造两个端点$v^e_{i}$与$v^e_{j}$,并将其分别连接在点$v_{i}$与$v_j$之上,如下图中所示(其中虚线表示$E$中的边),例如对于边$v_1 v_3$来说,我们为其构造了两个端点$v^{13}_{1}$与$v^{13}_3$并分别与$v_1$与$v_3$相连接。当然,很自然的,我们要求任意的边在进行绘制的时候,总是从我们为其构造的某个端点出发,一笔绘制到另一个为其构造的端点。
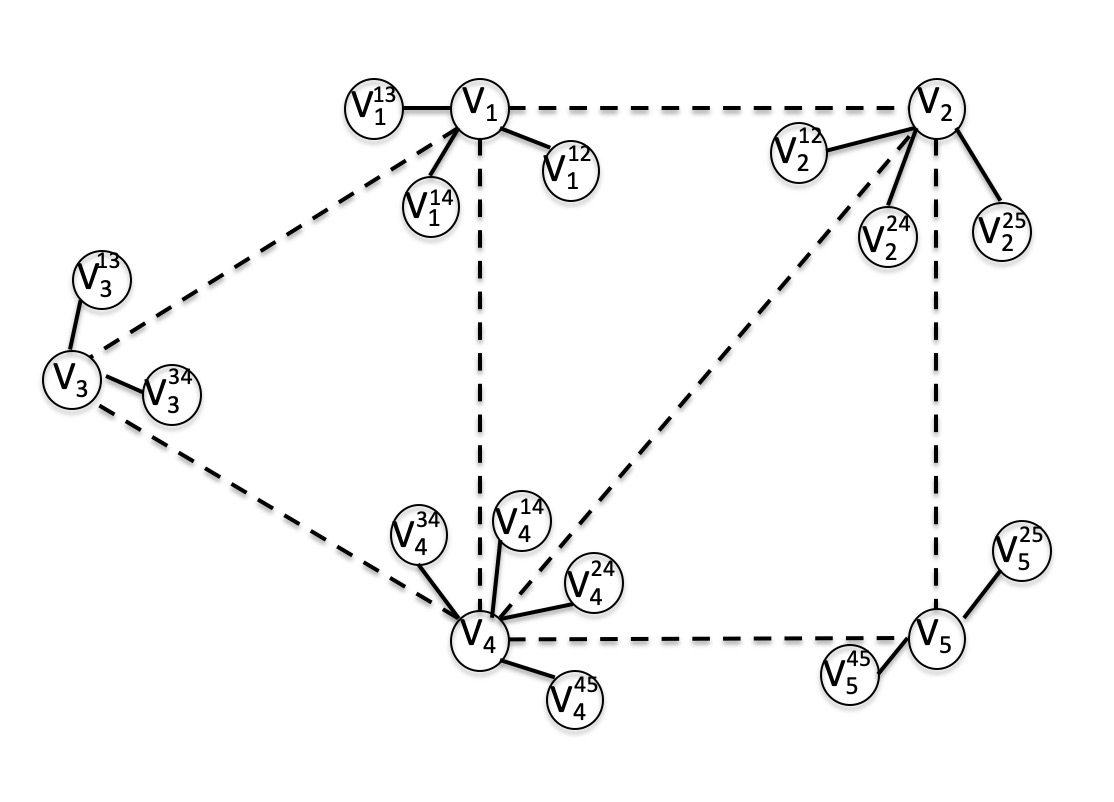
但仅仅是如此是不够的,我们必须要能实质性的去限制,这里我们首先构建一棵连接$G$中所有点的树$T_{V}$。下图给出了一个$T_{V}$的例子,这里我们将上面所构建的与边相关联的顶点也画上去了。注意到尽管我选择的$T_{V}$是图$G$的一棵生成树,但$T_{V}$中边并非一定要出现在$G$中,我们仅仅是希望有一棵连接$G$中所有点的树罢了,其更像是完全图$K_{\lvert V \rvert}$的一棵生成树。
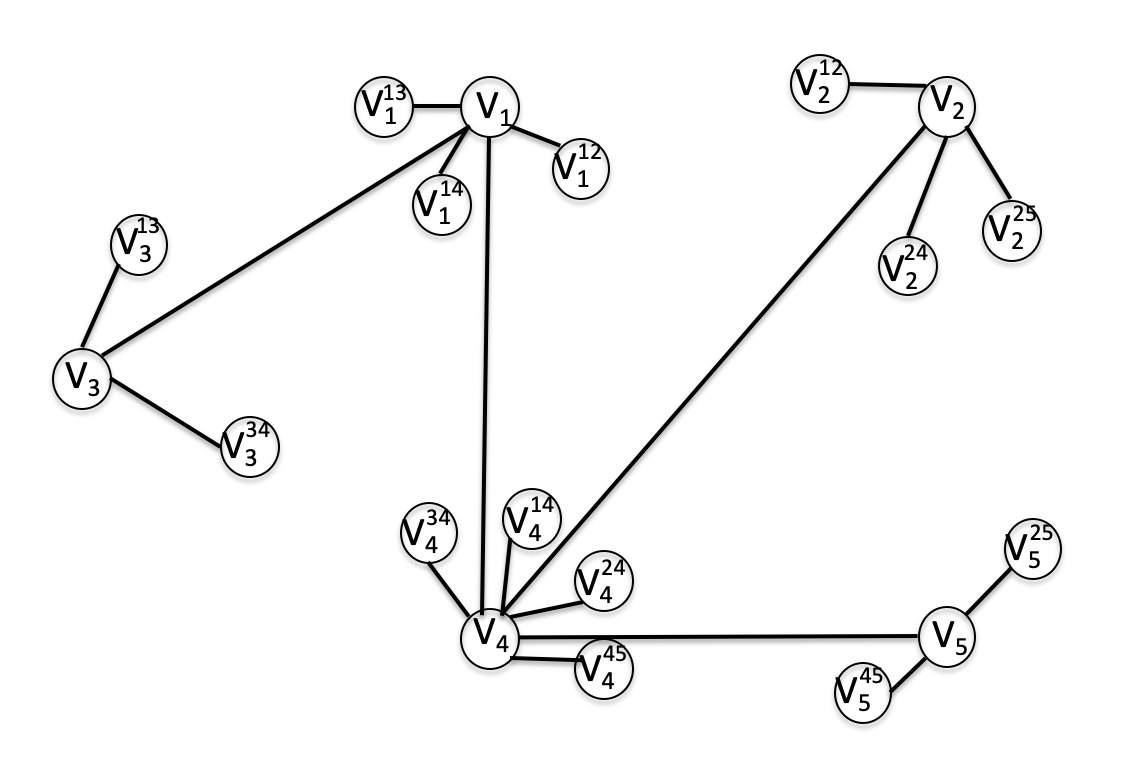
一旦树$T_{V}$被决定之后,我们首先将这棵树绘制在平面上—我们对于绘制这棵树并没有多大的限制,满足我们在第一节中提到的三点即可。而后,我们逐一将$G$的边进行绘制—此时便有一个限制了,我们不允许一条边$e \in E$在被绘制之时,与任意一条已经绘制的,$T_{V}$中的边发生交叉。
此时有趣的事情就来了,如下图所示,由于我们要求边在绘制之时不能与已经绘制的$T_{V}$发生交叉,端点的相对位置会直接决定两条边是否存在交叉。
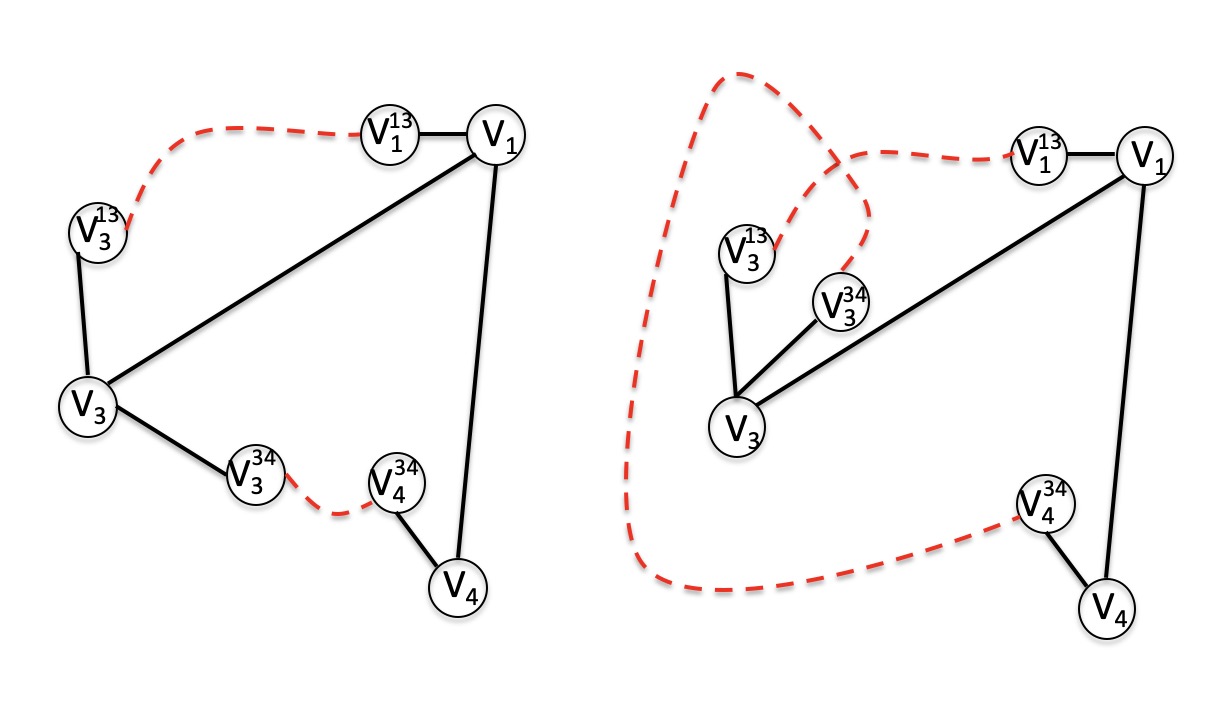
倘若我们以$T_{V}$中,到达$v_3$的边$v_1v_3$作为基准点,以逆时针方向来看,上左图中$v^{34}_3$在$v^{13}_3$之后,而上右图中在之前,其他点的相对位置不变的情况下,后者会导致交叉。这个观察告诉我们,两条边是否在绘制之后存在交叉,与我们所构建端点的相对位置息息相关。 作为基准点的边必须是到达当前点的边,因为这条边是唯一的—一个父亲能有多个孩子,而一个孩子只能拥有一个父亲。
那么这个要求是否会将一些$G$的可能描画给排除在外呢?这可能是我们最值得关心的情况,因为我们需要解决的是一个最优化问题,需要获得某种意义上最大或者是最小的解。这也意味着,倘若我们没有直接或者间接的验证每一个可行解,我们无法保证解的最优性。因此我们需要去证明,即便是如此限制之下,我们仍然能够得到$G$的每一种描画。
不过就像之前所讲的,我们今天不讲证明,但至少我们需要从想象力,从直觉上去感受一下命题的真伪。那么一方面考虑到$T_{V}$的任意性,另一方面考虑到一棵描画在平面上的树,是没有将平面分割成多个面的,因为树并不含圈。因此一棵绘制在平面上的树,会对你之后的描画产生任何影响吗?并不会。
那么我们该如何去决定这个相对位置呢?这实际上是需要我们对附着在点$v \in V$之上的,我们所构造的端点决定一个序。
图中点的序?很容易呀,使用深度优先搜索(DFS)不就可以做到了吗?
于是紧接着,我们构建上图的,从点$v_1$出发的一个DFS序,也即于某次深度优先搜索之时点被访问的顺序,如下图所示,对于任意一点$v$,我们以$DFS(v)$表示其被访问的次序,且对于附着在某点上所构建的端点$u$与$v$,倘若$DFS(u) < DFS(v)$,则我们认为在绘制之时,点$u$应在点$v$之前。
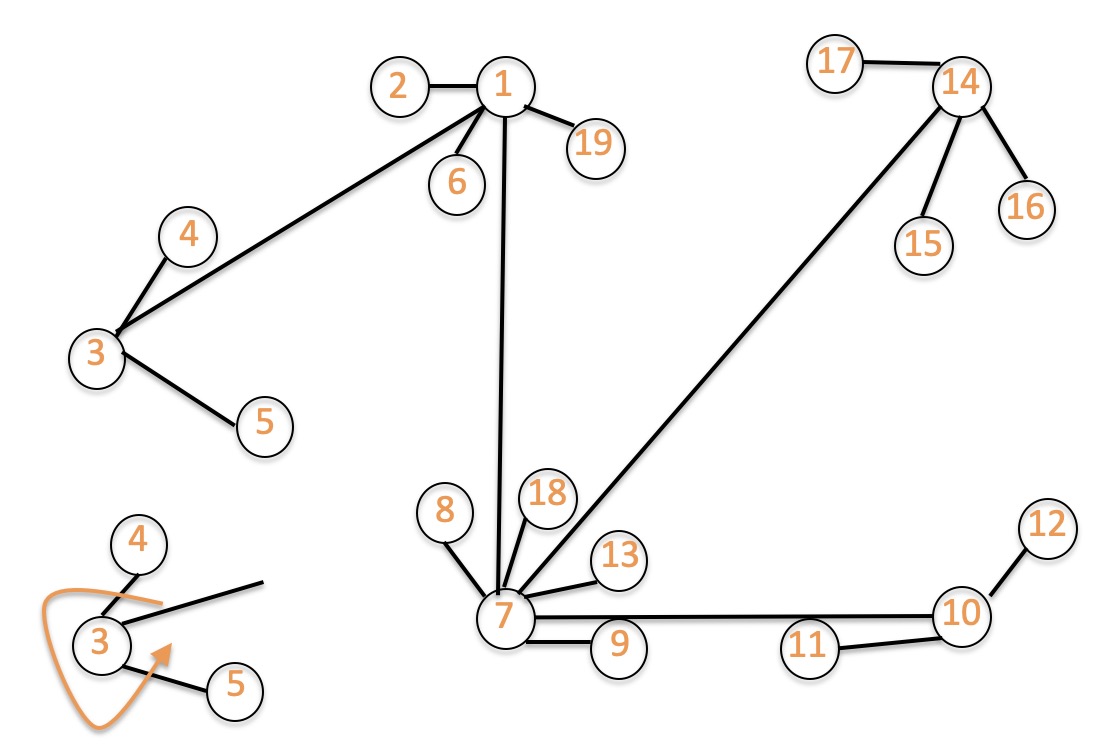
那么什么时候点$u$点$v$所关联的边与点$p$点$q$所关联的边会发生交叉呢?答案也很简单,从图中实际上也能很快的得到结论,假定$DFS(u) < DFS(v)$且$DFS(p) < DFS(p)$,此时交叉的充要条件即为
\[DFS(u) < DFS(p) < DFS(v) < DFS(q)\]对应到我们之前讲的例子的话,$u, v, p, q$也就分别对应$v^{13}_1, v^{34}_3, v^{13}_3, v^{34}_4$。
至此,图描画问题转变为了枚举生成树与DFS序的问题。
4.使用整数规划
将实际问题建模为整数规划并非什么新鲜事,不过在此之前,我们需要给出一些第三节中所描述的部分的严格定义。
给定一个无向图$G = (V, E)$,令$G’ = (V’, E’)$,其中,$V’ = V$且对于任意两点$u, v \in V’, uv \in E’$。 接着,对于每一条边$e = uv \in E$,我们创建两个点$u_e, v_e$并将边$uu_e, vv_e$加入$E’$中。
很显然,由我们在第三节所描述的,我们需要得到一棵$G’$的生成树$T’$,并于其之上决定一个DFS序。决定一棵生成树并不是什么新鲜的事情,许许多多的组合优化教科书上都会有提及。我们使用变量
\[y_{uv} \in \{0, 1\}, \forall u, v \in V'\]来表示边$uv$是否被选取到了生成树$T’$当中,即一条边$uv \in T$当且仅当$y_{uv} = 1$。
那么由生成树的性质我们可知,一共需要选择$\lvert V’ \rvert - 1$条边,即
\[\sum_{u, v \in V' \text{ s.t. } uv \in E'} y_{uv} = |V'| - 1\]我们以有根树的思想来考虑的话,每个点的入度至多只能为$1$,也即
\[\sum_{u \in V'} y_{uv} \le 1, \forall v \in V'\]至此,我们的生成树便决定好了。注意到在此语境下,实际上我们的生成树是一棵有根树,因为只选择$\lvert V’\rvert - 1$条边的情况下,一定会有一个点的入度为$0$,而其也就是事实上的根。考虑到对于决定DFS序而言,我们实际上是需要一个起点的,一棵有根树可谓是正中下怀。
当然,因为是有根树,$y_{uv}$与$y_{vu}$是不会同时为$1$的,尽管在无向图生成树的语境下他们俩的值应该相同,但无伤大雅。
接着便是建模所面临的的最核心的问题—DFS序该如何使用整数规划去决定。这里我们使用变量
\[z_{uv} \in \{0, 1\}, \forall u, v \in V'\]来表示每一对点$u, v$之间DFS序的大小关系,即$z_{uv} = 1$当且仅当$DFS(u) < DFS(v)$。
很显然,对于任意两点$u, v$,其之上的DFS序是可以相互比较的,因而$z_{uv}$实际上决定了一个全序(Total Order),其应满足完全性(Connexity)与传递性(Transitivity)。为此我们需要以下两条制约,
\[z_{uv} + z_{vu} = 1, \forall u, v \in V'\] \[z_{uv} + z_{vw} - z_{uw} \le 1, \forall u, v, w \in V'\]并且,只有当一条边$uv$被选择在生成树$T’$之中,我们才能在DFS的时候通过$u$抵达$v$。因此我们有,
\[z_{uv} \ge y_{uv}, \forall u, v \in V'\]同样的,由于树中任意两点之间的路径是唯一的,那么当我们存在两条边$(u, v), (p, q) \in T’$的时候,从$u$到达$q$的路径倘若存在,便只能是$u \rightarrow v \rightarrow p \rightarrow q$,这意味着我们有$DFS(u) < DFS(v) < DFS(p) < DFS(q)$,也就有
\[y_{uv} + y_{pq} + z_{up} + z_{pv} + z_{vq} \le 4, \forall u,v,p,q \in V'\]也即上述式子中五个变量不能同时为$1$。至此,我们的DFS序就定好了。接下来的事情就简单了,我们准备如下变量
\[x_{uv, pq} \in \{0, 1\}, \forall u, v, p, q \in V'\]那么当$uv$与$pq$分别代表原图$G$中的边时,$x_{uv, pq} = 1$当且仅当这两条边在绘制时发生了交叉。
那么由我们的第三节可知
\[x_{u_ev_e, p_fq_f} \ge z_{u_ev_e} + z_{p_fq_f} + z_{u_ep_f} + z_{p_fv_e} + z_{v_eq_f} - 4, \forall e = uv, f = pq \in E\]最后加上我们的目标函数
\[\text{Minimize: } \sum_{u, v, p, q \in V'} x_{uv, pq}\]便大功告成了。最终这个整数规划含有$\mathcal{O}(\lvert V \rvert^4)$个变量以及$\mathcal{O}(\lvert V\rvert^4)$条制约。
5.结语
尽管我们略过了证明而只讲述了基本想法,但实际上证明也并不复杂—但需要一些描画基础,枯燥乏味,因此也就没有必要执着于去书写严密的证明了。
在鄙人研究这个课题之前,于2006年有一篇论文给出了一种将计算交叉数的问题定式化为整数规划的方法,也几乎是该领域唯一一个切实可用的建模,其拥有指数条制约—因此当我们完成这个多项式条制约数的建模之时,实际上是非常期待能够有一个好的结果的。至于实际情况,建议大家使用CPLEX之类的求解器去自己尝试一番,想必也会是一个相当有趣的体验。
