算数・KMP算法

KMP算法（Knuth-Morris-Pratt Algorithm）

前言

说来惭愧，最近因工作需要给人讲解KMP算法，而途中却经常没法好好表述自己的想法，出一些哭笑不得的岔子。 于是决定试着写一篇简单的KMP算法介绍文，也权当是复习了吧。

1.问题

KMP算法是一个字符串匹配算法（String Matching Algorithm），用以在一个长字符串中，找出其是否包含一个或多个给定的字符串。 字符串匹配是一个非常经典的问题，因而细节部分就不再赘述了。 解决字符串匹配的一个简单而暴力的想法便是于长字符串的每个位置开始与给定字符串进行一一比较。 很显然，此种想法的时间复杂度将会是$\mathcal{O}(mn)$ — 倘若长字符串与给定字符串的长度分别为$m$与$n$的话。

2.观察

特殊情况总是灵感之源，在这里也不例外—很容易能够发现，当给定的字符串，我们姑且将其记做$p$，所包含的字符都互不相同的时候，我们是没有必要在每个位置都进行一一比较的。 比如下列情况（图1）中，这里字符串$p = \text{abcdefgh}$，于某次对比的过程中，我们发现字符’h’与数字’4’不匹配，按照之前的做法，我们将$p$右移一位重新进行比较。 而事实上，由于我们已经知道字符’h’与字符串$p$中的每一个字符都不相同，更加明智的做法是跳过’h’之前的字符，直接将字符串$p$右移7位，如图1中所作的那样。

不过，我们并非能够总是如此幸运，一串各个字符互不相同的字符串是可遇而不可求的。 顺着上面的思路，我们很容易能构造出如下（图2）情况，这里字符串$p = \text{abc1abc2}$，当字符’1’与字符’2’不匹配时，由于字符串$p$中存在着一些相同的片段（例中为’abc’），我们不能够像图1中那样简单粗暴的将字符串$p$右移7位，而是只能如图中所示一般右移4位，重新开始比较。

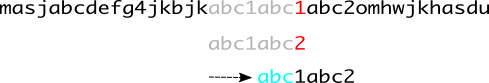
那么更一般的情况是怎样的呢？考虑到我们总是需要从字符串$p$的第一个字符进行比较，这个相同的片段似乎总是需要出现在$p$的头部与尾部，从而使我们能够构建出如下（图3）的一般情况—当我们在红色处失配时，注意字符串$p$中由开始到红色处的这部分，倘若于这部分中，头尾有着相同的片段（也即图中的天蓝色部分，由于其出现在头尾，我们姑且称其为前缀与后缀），则我们直接将字符串$p$的头部移动到后缀所在的地方，开始新的匹配。

话虽如此，前后缀应该如何截取仍然是一个待考量的问题。因为一次移动的尺度可能会很大，而导致我们错过了正确的匹配位置。 我们假设在后缀之前的某个位置存在一个合法匹配，并将字符串$p$的头移动至这个位置（图4）。 则此时，图中的紫色片段同时出现在字符串$p$的头尾，将会是更大的前后缀。 因而我们每次须选取最大的前后缀以避免这种情况。

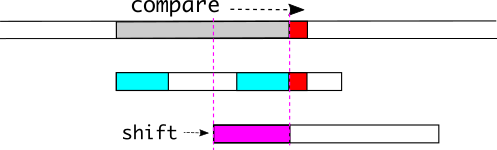
而这，也就是KMP算法的基本思想。注意到对于长字符串中的每一个字符来说，无论它与给定字符串中的哪个字符进行了比较，要么当前进行比较的位置向右移动一位，要么给定字符串至少向右移动一位。而由于给定字符串向右移动的距离始终受限于当前进行比较的位置， 该算法的复杂度与长字符串的长度呈线性关系，即$\mathcal{O}(m + n)$ — 同样的，假定长字符串与给定字符串的长度分别为$m$与$n$的话。

3.解决

在落地我们的思想之前，我们首先将之前提到的一些概念形式化一下。

3.1.定义

令$A$为一个字符集且$s = s_0s_1 \ldots s_{m-1}, m \in \mathbb{N}$是一个$A$上的字符串，对于整数$l, r \in [0, m-1], l \le r$，我们使用$s[l,r]$表示子串$s_l\ldots s_r$，且有

     (1) 我们称$s$的一个子串$a$是其前缀（Prefix） 如果有$a = s[0, i-1], i \in [0, m - 1]$

     (2) 我们称$s$的一个子串$b$是其后缀（Suffix） 如果有$b = s[m-i,m-1], i \in [0, m - 1]$

     (3) 我们称一对$s$的子串$(a, b)$是其边界（Border） 如果有$a = b$且$a$与$b$分别为$s$的前后缀。一个边界的宽度（Width） 为子串$a$的长度，记做$\lvert (a, b) \rvert$。

那么对于字符串$s = \text{abcab}$来说，其前缀为

其后缀为

其边界为

3.2.实现

进而问题的核心便是，给定一个整数$i \in [1, m-1]$，我们如何能够计算得到子串$s[0,i-1]$的最大边界。

令$b_i$为子串$s[0,i-1]$的最大边界的宽度，由于当子串为空的时候不存在边界，我们将$b_0$设置为$-1$。

那么倘若$b_0, b_1, \ldots, b_{i-1}$均已算出，我们该如何计算出$b_{i}$的值呢？ 事实上，由于边界中的前后缀是两个相同的子串，因此我们只需要检查$s_{b_{i-1}}$与$s_{i-1}$是否相同（如图5）。倘若相同，则$b_i = b_{i - 1} + 1$，这是我们希望看到的情况。

倘若不同，我们便需要去寻找一个新的边界，它的宽度至多只有$b_{i-1}$。 为了快速求得这个边界，我们需要另一个微小的发现，其表述如下：

令$(a_1, b_1), (a_2, b_2)$为字符串$s$的两个不同的边界，且有$\lvert(a_1, b_1)\rvert < \lvert(a_2, b_2)\rvert$，则$(a_1, b_1)$同样是子串$a_2$（或$b_2$）的边界。

证明实际上是相当容易的 — 因为子串$a_1, b_1$分别是子串$a_2, b_2$的前缀与后缀。

有了这个发现，我们需要检查的位置便只剩$b_{i-1}, b_{b_{i-1}}, \ldots$。

最终，这个过程的实现看起来会是下面这个样子的。

void preprocess(char s[], int b[], int m) {
    b[0] = -1;
    for (int i = 0, j = -1; i < m;) {
        while (j >= 0 && s[i] != s[j]) { j = b[j]; }
        i++, j++;
        b[i] = j;
    }
}

这里while循环的执行次数严格受限于变量j的值，因为每次循环变量j的值至少会减少1. 而变量j唯一增量在for循环中的i自增之后，这使得j的总增量为$m$，因而while循环执行的总次数至多为$m$次。 即该实现的复杂度为$\mathcal{O}(m)$。

这也便是我们在2节最后所提到的“给定字符串向右移动的距离始终受限于当前进行比较的位置”。

有了$b_i$，KMP算法的实现就非常简单了，它看起来是这个样子的。

void kmp(char p[], int m, char s[], int n) {
    int b[m];
    preprocess(p, b, m);
    for (int i = 0, j = 0; i < n;) {
        while(j >= 0 && s[i] != p[j]) { j = b[j]; }
        i++, j++;
        if (j == m) { /* Found */ }
    }
}

他看起来和计算$b_i$差不多，而这实际上是因为$b_i$的计算是某种意义上的自我匹配。 同样的，对于while循环的分析实际上对应着我们在2节最后所提到的“给定字符串向右移动的距离始终受限于当前进行比较的位置”。 因此，KMP算法的复杂度为$\mathcal{O}(m + n)$。

4.后记

至于KMP算法真正的灵感之源，我也无从知晓，只能是装模作样的写了点自己的想法—实际上这篇算是相当偷懒了，再加上各处优秀的KMP算法讲解很多，算是一篇相当无用的轮子文。 印象中我初次接触KMP算法的时候还费了不少劲才理解，也当做是对于那时上进的我的纪念吧，愿自己能在有生之年填完那些远古巨坑。