强化学习(Reinforcement Learning)其三・AlphaGO
前言
好的,终于来了!
AlphaGO可谓深度强化学习应用中第一个集大成者,使用到了当时几乎所有大家能够想到的技巧,并通过与李世石的对战,刷新了普通人对于人工智能发展的认知,也点引爆了整个资本市场,是深度学习发展史上的里程碑之一。 如同强化学习篇章开始时所承诺的那样,今天就让我们来认真学习一下,AlphaGO究竟是怎样炼成的。
1.环境与网络结构
对于围棋本身或许不用太多说明。我们将围棋棋盘看做是一个$19 \times 19$的矩阵,矩阵的每个位置便可以对应棋盘上每个位置,通过不同的数字对棋局信息进行表达。 在AlphaGO中,我们使用共计$48$个矩阵对包括最近$7$轮的棋谱,对手与自己的着子,以及被称之为“气”的信息。 也就是说,智能体从环境所观测到的状态(State,或者说策略网络的输入)是一个$19 \times 19 \times 48$的张量,包含了直接或者我们人为进行抽象的,棋盘上的各种信息,其详细构成如下表所示
\[\begin{array}{ccc} \hline \text{Feature} & \text{#planes} & \text{Description} \\ \hline \text{Stone colour} & 3 & \text{Player stone / opponent stone / empty } \\ \text{Ones} & 1 & \text{A constant plane filled with $1$} \\ \text{Turns since} & 8 & \text{How many turns since a move was played} \\ \text{Liberties} & 8 & \text{Number of liberties (empty adjacent points)} \\ \text{Capture size} & 8 & \text{How many opponent stones would be captured} \\ \text{Self-atari size} & 8 & \text{How many of own stones would be captured} \\ \text{Liberties after move} & 8 & \text{Number of liberties after this move is played} \\ \text{Ladder capture} & 1 & \text{A move at this point is a successful ladder move} \\ \text{Ladder escape} & 1 & \text{A move at this point is a successful ladder escape} \\ \text{Sensibleness} & 1 & \text{A move is legal and does not fill its own eyes} \\ \text{Zeros} & 1 & \text{A constant plane filled with $0$} \\ \hline \text{Player colour} & 1 & \text{Whether current player is black} \end{array}\]而策略网络本身也非常的简单,粗略的结构如下图所示
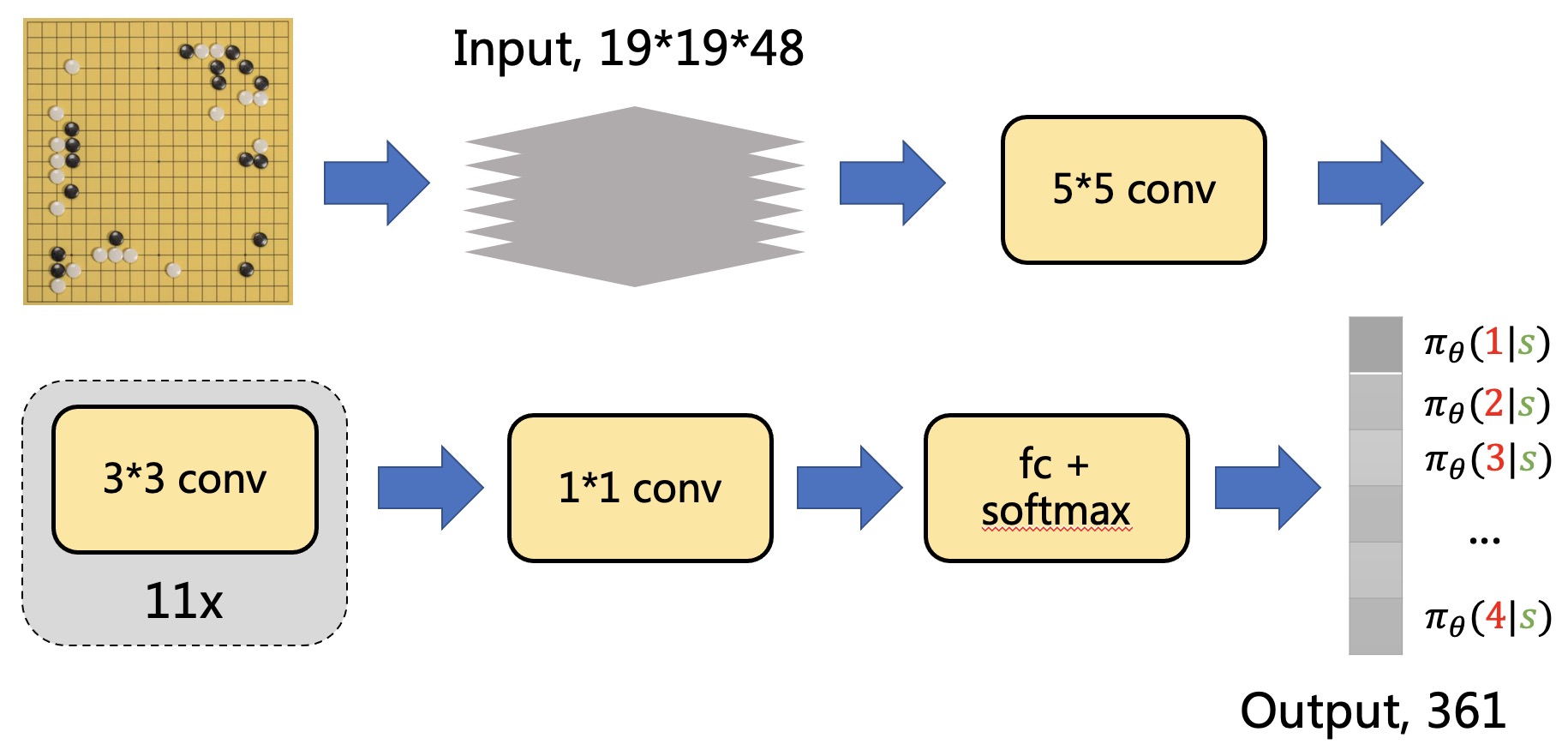
我们使用$\pi_{\theta}$来表示我们的策略网络, 网络的参数为$\theta$,如我们一贯所做的那样。 策略网络的输出是一个$1 \times 361$的张量,对应棋盘上各个位置的着子概率。
2.模仿学习
初版AlphaGO中,研究者们利用KGS上160万高手的棋谱,首先使用传统的监督学习对策略网络进行训练,让我们的智能体学习高手们的下法。 对于给定的状态$s$,我们使用$\pi_\theta (s)$与棋谱实际着子位置的独热(one-hot)编码的交叉熵作为损失函数,对网络进行训练更新。
对于不少复杂的任务来说,学习前辈们的经验,或是给予某种引导,或是提供一些原本环境中不可见的信息来帮助,是强化学习中惯用的技巧。
3.策略梯度
实际上通过模仿学习所得到的策略网络已经能够打败绝大多数人了(能力大约在六段至七段之间的水平),但无法做到“青出于蓝而胜于蓝”。 为此,我们接下来要使用在[策略学习][myyura_policy_leraning]所讲述的方法,对我们的策略网络进行进一步的训练。
我们简单回顾一下策略学习的算法流程:
Algorithm parameters: learning rate $\alpha \in (0, 1]$
- Observe state $s_t$
- Randomly sample action $a_t$ according to $\pi_{\theta}(\cdot \mid s_t)$
- Estimate action-value $Q^{\pi_{\theta}}(s_t,a_t)$
- Approximate policy gradient $\frac{\partial \log \pi_{\theta} (a \mid s)}{\partial \theta} Q^{\pi_{\theta}}(s,a)$
- Update policy network $\theta \leftarrow \theta + \alpha \frac{\partial \log \pi_{\theta} (a \mid s)}{\partial \theta} Q^{\pi_{\theta}}(s,a)$
在策略学习中,对于给定的状态$s_t$与采取的动作$a_t$,我们需要估计动作价值$Q^{\pi_{\theta}}(s_t,a_t)$。 在AlphaGo中,我们使用REINFORCE方案对动作价值进行估计,即先使用策略网络打完整局游戏(这里不妨假设我们在这局游戏中一共执行了$n+1$步),然后使用
\[R(\tau) = \sum_{i=0}^n \gamma^i r_i\]作为动作价值的估计。
那么AlphaGO中是如何设计奖励函数的呢?
DeepMind的研究者们认为,对于一局没有结束的游戏,我们往往很难从盘中去准确评价每一次着子的好坏,因此对于一局在第$n+1$步结束的游戏,我们置
\[\begin{align*} & r_0 = r_1 = \cdots = r_{n-1} = 0 \\ & r_n = +1, \text{if win} \\ & r_n = -1, \text{if lose} \end{align*}\]且回报折扣$\gamma=1$。 在这种设置下,若获胜,我们有
\[R(\tau_0) = R(\tau_1) = \cdots = R(\tau_n) = +1\]若失败,则有
\[R(\tau_0) = R(\tau_1) = \cdots = R(\tau_n) = -1\]也就是说,由于我们不知道一局棋中究竟哪一步是好棋,哪一步是臭棋,因此我们就纯粹结果论—如果我们赢了,则认为每一步都是好棋,如果我们输了,则认为每一步都是臭棋。 对于好棋与臭棋的评价会直接作为我们对动作价值的估计,从而在策略梯度中增加(或减少)对应着子的概率,且增加与减少的幅度是相同的。
因而可以知道的是,如果我们执行足够多的对局,好棋终会脱颖而出,成为主要备选项。
4.状态价值与蒙特卡洛树搜索
在围棋对局,尤其是高手对局中,往往一个小小的失误就会使得满盘皆输。 为了尽可能降低我们神经网络抽风的概率,我们需要使用一种被称之为蒙特卡洛树搜索(Monte Carlo Tree Search,MCTS)的方式来选择我们的动作,而非直接基于策略网络进行选择。
在介绍MCTS之前,我们需要进行一些准备工作—训练得到一个状态价值网络$V_w (s)$(其中$w$为该网络的参数)。
4.1.状态价值网络
状态价值网络的结构几乎与策略网络相同,仅将最后全连接层的输出维度更改为1,并移除了SoftMax。
根据状态价值的定义,假设我们使用策略网络$\pi_\theta$打完某局在第$n+1$步结束的游戏,那么给定的状态$s_t$,回报$R(\tau_t)$即可作为状态价值的估计,因此损失函数的构建也非常简单,如下所示
\[\frac{1}{2}\sum_{t=0}^n (V_w(s_t) - R(\tau_t))^2\]4.2.蒙特卡洛树搜索
蒙特卡洛树搜索一共包含四个步骤,选择(Selection)、扩展(Expansion)、仿真(Simulation)与回溯(Backup)。
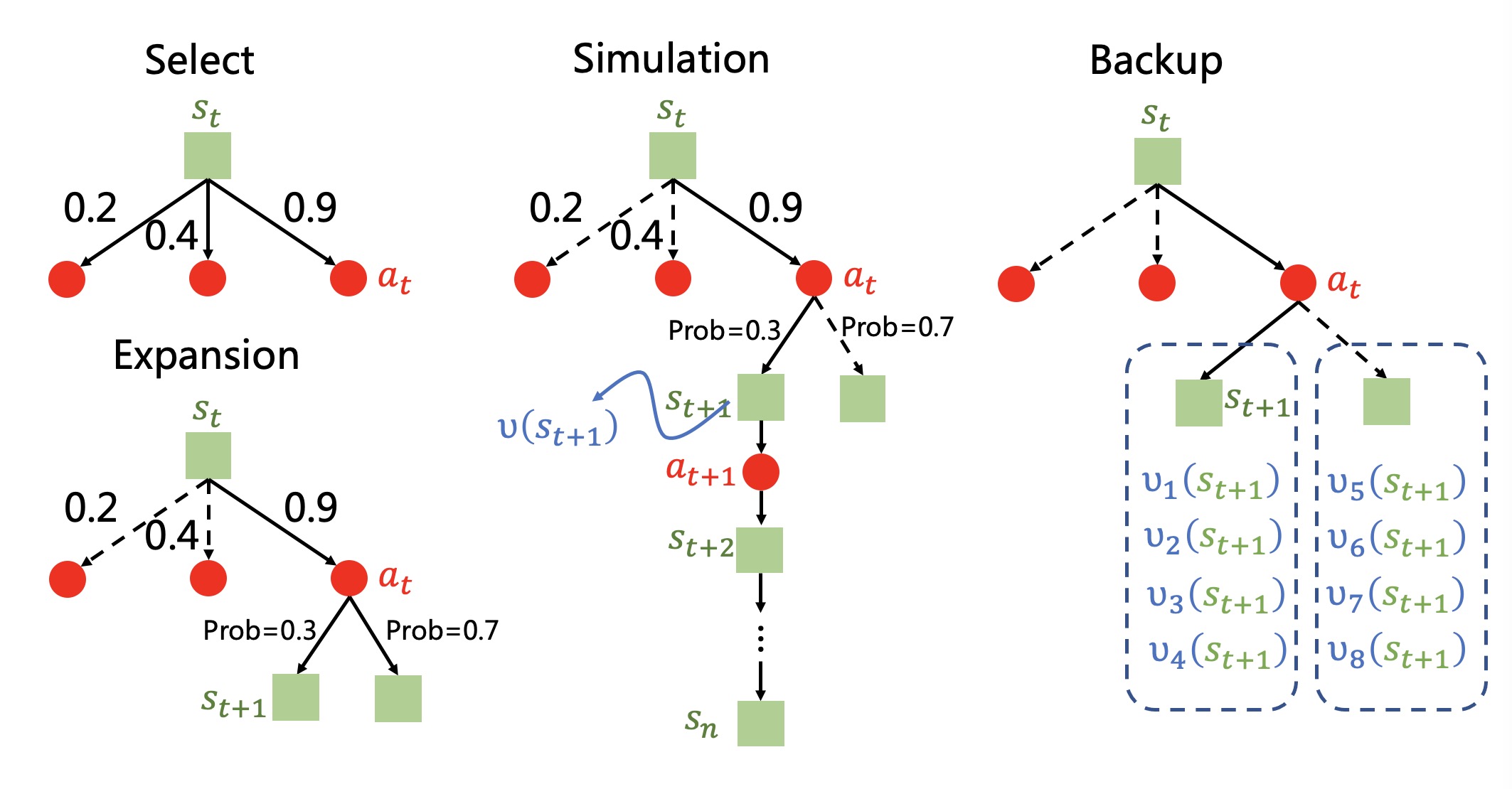
对于给定的状态$s_t$,我们会基于一个预先定义的动作分值函数score$(a)$ 选择分数最高的动作$a_t$,这个过程被称之为选择。
在动作$a_t$被执行之后,局面会被更新。 注意到此时的局面指的是“对手”需要着子的状态,并非指的是我们在执行动作$a_t$之后所面临的下一个需要“我们”着子的状态。
我们将对手需要着子的状态记做$s^{\prime}_t$,与$s_t$相对应。
于是“我们”以自我博弈的方式,继续使用策略网络$\pi_{\theta}$ 作为“对手”进行着子(直接使用概率最高的动作即可),使得状态更新至$s_{t+1}$。 这个过程被称之为扩展。
接着,我们计算状态价值$V_w (s_{t+1})$, 并自我博弈直至游戏结束,得到回报$R$。 这里或许是考虑到估计的状态价值与实际可能存在较大偏差,文章中取了真实观测值与估计值的平均数,使用$v(s_{t+1}) = \frac{1}{2} (V_w (s_{t+1}) + R)$作为状态$s_{t+1}$的整体评价。 这个过程被称之为仿真。
最后,我们回溯至开始选择动作$a_t$的时候,对$a_t$的分数进行如下更新
\[\text{score}(a_t) = P(a_t) + \eta \frac{\pi_\theta (a_t\mid s_t)}{1 + N(a_t)}\]其中$N(a_t)$是$a_t$被重复选择的次数—在整个蒙特卡洛树搜索过程中,上述四个步骤会被执行成千上万次。该项用以平衡每个动作被采样到的概率,避免某些动作被反复采样,无法搜索到更多变化。
而$P(a_t)=\text{mean} \sum v(s_{t+1})$,为这数千次尝试中下一个状态的平均估计价值,用以评价当前选择动作的好坏。 $\eta$为超参数,用以手动平衡上述二者的重要性。
从score$(a)$的定义可以看出来,那些能够为我们接下来带来好局面的动作会更容易被采样到,而这也正式我们所期望的。 因此,最终我们选择在蒙特卡洛树搜索中被选择最多的次数的动作,作为我们最终的选择。
蒙特卡洛树搜索的本质,便是通过大量的自我博弈,去逼近真正的最优解—就像我们用蒙特卡罗方法去逼近圆周率$\pi$一样。 比起直接使用策略网络输出的结果,在保证充分多的尝试次数的情况下,我们可以认为蒙特卡洛树搜索得到的结果总是“不坏于”策略网络的输出结果的。 因此,蒙特卡洛树搜索可以显著提升对局着子的稳定性,或者说下限。
这里很自然的会出现一个疑问,为什么我们不在训练过程中就用上这么好的搜索方法呢?实际上在之后改进的AlphaZero中,研究者们便将蒙特卡洛树搜索加入到了训练过程中,并去除了包括“气”,模仿学习等需要人类专家经验的部分,这便是后话了。
5.后记
道阻且长。
