图论(Graph Theory)其一・基本定义及其表示(Definitions and Representations)
前言
好的今天我们讲图论—不对,应该说是图论学习笔记。 昨天在一个相当简单的图论题目上折腾了两个多小时,让我对自己不扎实的基础感到非常痛心,痛定思痛,决定复习一下。 当然,说是学习笔记,我想最后应该会变成自选主题的,满是自娱自乐的杂谈。
1.基本定义
第一部分我们会介绍一些有关于图论中的基本定义。 图的定义是一个很奇怪的东西,十本书中可能会看到九种不同的写法。 考虑到以后的内容应该会主要集中在简单图,因此我们用一种相当简略的定义—我们认为图$G$即为一个有序的二元组$(V, E)$, 其中$V$是一个非空有限集,也称之为点集(Vertex Set),而$E$则为点集中的元素的二元组的多重集合(Multi-Set),通常称之为边集(Edge Set)。
举例来说,我们有图$G = (V, E)$,那么点集$V$和边集$E$应该看起来是下面这样子的
\[\begin{align} V &= \{v_1, v_2, v_3, v_4, v_5\}\\ E &= \{v_1v_2, v_2v_3, v_3v_3, v_3v_4,v_2v_4, v_4v_5, v_2v_5, v_2v_5\} \end{align}\]这个例子实际上是我从Graph Theory with Applications - J.A.Bondy & U.S.R.Murty中抄过来的—以我们定义的形式。 有时我们也会用$V(G)$与$E(G)$来分别表示图$G$的点集与边集。
我们可以通过如下形式将这张图画在平面上,并给边安排上一些名字—相信绝大多数人最初是以这种方式认识到图的
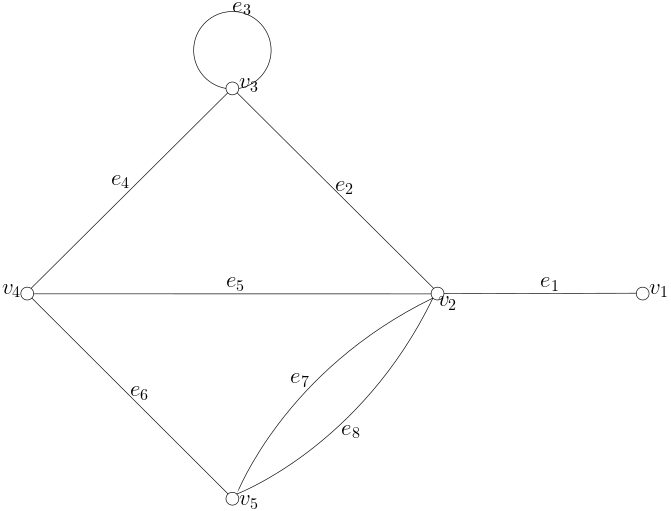
可以看到,图中有一些看起来相对特殊的情况。 例如边$e_3 = v_3v_3$,是一条“自己连接着自己的”的边,我们把这样的边称为自圈(Self-Loop)。 此外,边$e_7$与$e_8$实际上是两条相同的边,我们把这种情况称为多重边(Multi-Edge)。
而我们主要想要关注的,实际上是不包含自圈与多重边的图,我们通常称这样的图为简单图(Simple Graph)。
回忆一下我们对于边集的定义,其为一个一个二元组的多重集,而二元组实际上是可以有序的(Ordered)。 倘若我们认为边集中的二元组有序,即认为$v_1v_2$与$v_2v_1$不再是同一条边,则我们称其为有向图(Digraph),与其相对应的则称之为无向图(Undigraph)。 为了区分二元组是否有序,通常以$(v_1, v_2)$的形式表示有序元组,区别于$v_1v_2$。 在绘制时,边$(v_1, v_2)$会被绘制为一条由点$v_1$指向$v_2$的边。
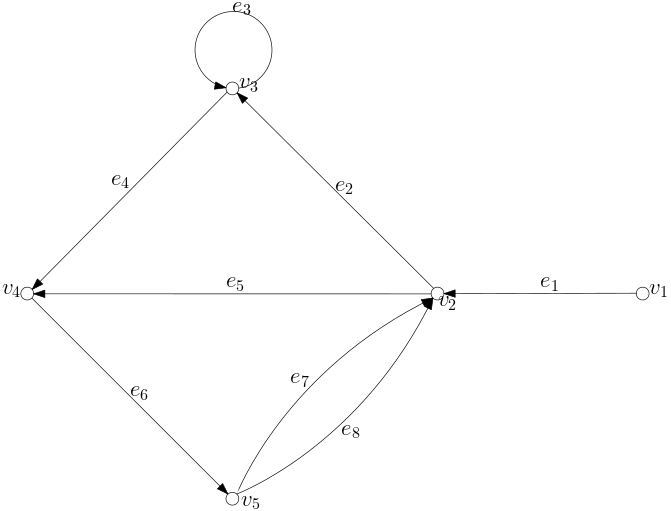
对于一点$u \in V$,与其邻接的边的数量被称为点$u$的度(Degree),记做$d(u)$,例如上述无向图中点$v_2$,其度为$5$。 在有向图中,考虑到边有了方向,我们将其分别讨论—由$u$指向其他的点的边的数量,称为出度(Outdegree),反之称为入度(Indegree),分别记做$d^+(u)$与$d^-(u)$,例如上述有向图中的点$v_2$,其出度与入度分别为$2$与$3$。
而与一点$u \in V$相邻接的点的集合被称为$u$的邻居(Neighbor),记做$N(u)$。对应的,在有向图中,我们以$N^-(u)$与$N^+(u)$分别表示以指向$u$的边邻接的点的集合与由$u$指向的边邻接的点的集合。 不难看出,简单无向图的情况下,有$d(u) = \lvert N(u) \rvert$。
不特殊提及的话,我们总是讨论简单无向图。
在简单图中,我们也会关注几种相对特殊的情况—例如任意两点之间均有边的情况,我们把这样的图称为完全图(Complete Graph)。 很显然对于$n$个点的完全图,其将会有$n(n-1) / 2$条边,这也是$n$点的简单图所能具有的最大边数。
再比如,倘若点集$V$可以被分割为两部分$X, Y \subset V$且有$X \cup Y = V, X \cap Y = \emptyset$,使得对于任意一条边$e = uv \in E$,要么$u \in X, v \in Y$,要么$u \in Y, v \in X$。 就像下面这样,
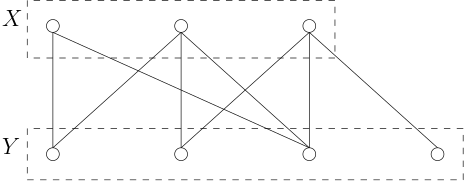
则我们把这样的图称为二分图(Bipartite Graph),通常也会记做$G = ((X, Y), E)$。 同样的,若对于任意两点$u \in X, v \in Y$,均有$uv \in e$,则我们称这样的二分图为完全二分图,而完全二分图拥有$\lvert X \rvert \lvert Y \rvert$条边。
学会计算/估计一张图所具有的边数,对于我们之后进行图算法的算法分析是很有帮助的,因此顺着上面二分图的定义,让我们来看一个稍微复杂一点的。
很容易的能够将二分图的定义拓展到$k$分图(k-partite Graph)。 于是我们来思考一种非常特殊的完全$k$分图,在其中$n$个点被非常均匀的分成了$k$部分—每一部分要么具有$\lfloor \frac{n}{k} \rfloor$个点,要么具有$\lceil \frac{n}{k} \rceil$个点。
考虑到只有不同分割中的点之间能够存在边,倘若知道每个分割的点的数量,简单的乘法即可完事。 因而问题的关键在于每个分割究竟有多少点,换句话说,具有$\lfloor \frac{n}{k} \rfloor$个点的分割与具有$\lceil \frac{n}{k} \rceil$个点的分割分别有多少。
这是一个简单的问题,我们有$n - \lfloor \frac{n}{k} \rfloor k$个具有$\lfloor \frac{n}{k} \rfloor$个点的分割,因而有$k - n + \lfloor \frac{n}{k} \rfloor k$个具有$\lceil \frac{n}{k} \rceil$个点的分割。
令$m = \lfloor \frac{n}{k} \rfloor$,那么对于$m$个点的分割来说,其中每个点会与分割外的$n-m$个点相连,因此有$m(n - m)(k - n + mk)$条边。 同理对于$m+1$个点的分割来说,一共有$(m+1)(n - m - 1)(n-mk)$条边。
每条边会被重复计算一次,因此答案为
\[\begin{align} &(m(n - m)(k - n + mk) + (m+1)(n - m - 1)(n-mk)) / 2 \\ &=\binom{n - m}{2} + (k-1)\binom{m + 1}{2} \end{align}\]集合有子集,图同样有着子图(Subgraph)的概念。 令图$G’ = (V’, E’)$,其中$V’ \subseteq V$,$E’ \subseteq E$,则此时我们称$G’$为$G$的子图。 形象的说,像是从图$G$中取出来的一部分。
如现实中的地图一样,我们也可以定义路径(Path),来描述两点(地)之间的可达性。
图$G = (V, E)$中一条点$u$到点$v$的路径$P_{u,v}$指的是一组点的序列$(u=w_0, w_1, w_2, \ldots, v=w_k)$,其中序列的首尾分别为$u$与$v$,且对于相邻的两点$w_i, w_{i+1}$,有$w_iw_{i+1} \in E$。 倘若$u = v$,即一条自己到自己的路径,则我们称该路径为圈(Cycle)。 当然,如上一节中我们提到的简单图,我们同样也可以定义简单路径—路径中的点互不相同。
有向图中也一样,不过是将$w_iw_{i+1} \in E$对应的修改为$(w_i, w_{i+1}) \in E$,而此时我们也会称路径为有向路径,如同单行道一般。
倘若图中任意两点间均存在一条路径,则我们称图为连通的(Connected),反之则为不连通的(Unconnected)。 上面例子中所提到的$G$很显然是连通图,倘若我们从中去掉边$e_2, e_5$与$e_6$,如下图所示,则为不连通图。
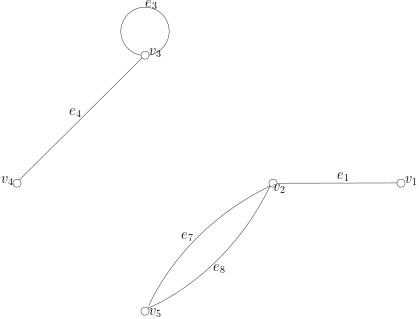
对于一个不连通图$G$来说,其中一定存在若干连通部分(如上图中的左上右下),每个部分为该不连通图的子图,且该部分无法通过加入一条图$G$中的边使其成为一个更大的$G$的连通子图。 我们把这样的“极大的连通子图”成为图$G$中的连通分量(Connected Component)。 而图$G$所具有的连通分量的数量记做$\omega(G)$。
若从连通图中移除某个(条)顶点(边),会使得该连通图变得不连通,则我们称这样的点(边)为切点Cut Vertex(切边Cut Edge)。
接下来我们介绍图同构(Graph isomorphism),观察下面这张图,我们将其记做$H = (V_H, E_H)$,
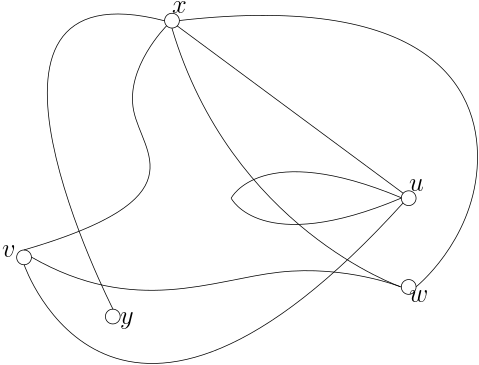
他与我们最开始介绍的图例$G = (V, E)$一样,拥有$5$个点,$8$条边。 且倘若你细心的话,你会发现尽管两张图看起来天差地别,但其实具有相同的结构—我们可以找到一个映射$\phi: V \rightarrow V_H$,使得对于任意一条边$uv \in E$,我们都有$\phi(u)\phi(v) \in E_H$,即
\[\begin{align} \phi(v_1) = y, \quad \phi(v_2) = x, \quad \phi(v_3) = u, \quad \phi(v_4) = v, \quad \phi(v_5) = w \end{align}\]此时我们说图$G$与图$H$是同构的(Isomorphic),记做$G \simeq H$—换言之,真正差异之处只有点与边的名字。 若有$G = H$,即图到其自身的同构,我们称之为图的自同构(Automorphism)。
2.图的表示
对于任意的图$G = (V, E)$—这里我们就姑且只考虑简单图了—假定其点集$V = \{ v_1, v_2, \ldots, v_n \}$,我们可以用一个矩阵$A$来表示它,其中$A_{ij} = 1$当且仅当$v_iv_j \in E$。 假定点集和边集分别为
\[\begin{align} V &= \{v_1, v_2, v_3, v_4\} \\ E &= \{v_1v_2, v_2v_3, v_3v_4, v_4v_1, v_1v_3\} \end{align}\]其对应的矩阵则为
\[\begin{pmatrix} 0 & 1 & 1 & 1\\ 1 & 0 & 1 & 0\\ 1 & 1 & 0 & 1\\ 1 & 0 & 1 & 0 \end{pmatrix}\]我们把$A$称作$G$的邻接矩阵(Adjacent Matrix)。
在邻接矩阵表示一张图之前,它首先是一个矩阵,这暗示我们其作为矩阵本身所被定义的一些运算在其表示图时也可能会具备一些特殊含义。 考虑到矩阵乘法是这之中最基础而又特殊的,我们来看看邻接矩阵$A$的幂,是否具有什么特殊的信息。
由矩阵乘法的定义,我们有
\[A^2_{ij} = \sum_{k} A_{ik} A_{kj}\]考虑到仅当$A_{ik}$与$A_{kj}$均为$1$时,其乘积方为$1$。 这意味着存在一条$v_i$到$v_k$的路径和一条$v_k$到$v_j$的路径—即存在一条$v_i$到$v_j$的,长度为$2$的路径。 于是$A^2_{ij}$所代表的含义便是点$v_i$到点$v_j$的长度为$2$的路径条数—不过需要注意,这里不仅仅是简单路径。
还有更多吗?—实际上不仅仅是幂,邻接矩阵的特征值也能够和我们之前讲的某些定义联系起来
令$G$是一个拥有$n$个点的简单图,矩阵$A$为$G$的邻接矩阵。若$A$的特征值(于复数域上)互不相同,则$G$的自同构群是阿贝尔群(即可交换的)。
证明:从图同构的定义出发,很容意识到其自同构是一个置换矩阵(Permutation Matrix)$P$使得$PAP’ = A$。 且因置换矩阵$P$为正交矩阵,因此有$P’ = P^{-1}$,进而有$AP = PA$。
因此,假定$P,Q$为$G$的自同构群中任意两个元素,则我们有$AP = PA$且$QA = AQ$。 且由于$A$具有互不相同的特征值,其应与对角矩阵$D = \text{diag}(d_{11}, d_{22}, \ldots, d_{nn})$相似,其中$d_{ii} \neq d_{jj}$对于任意的$i \neq j$。
于是我们有$A = S^{-1}DS$对于某个可逆矩阵$S$,进而有
\[\begin{align} P(S^{-1}DS) &= (S^{-1}DS)P \\ (SPS^{-1})D &= D(SPS^{-1}) \end{align}\]对于一个矩阵$X$,我们用$(X)_{ij}$来表示矩阵的第$i$行第$j$列的元素,且令$X_P = SPS^{-1}$则有
\[\begin{align} (X_P D)_{ij} &= (X_P)_{ij} \times d_{ii} \\ (D X_P)_{ij} &= (X_P)_{ij} \times d_{jj} \end{align}\]考虑到当$i \neq j$时,$d_{ii} \neq d_{jj}$,因而此时有$(X_P)_{ij} = 0$,即$X_P$是一个对角矩阵。 同理,$X_Q$也是一个对角矩阵,因此有$X_P X_Q = X_Q X_P$,也就有$PQ = QP$,命题得证。
3.后记
这篇本来计划只是记录一些基本的定义随后使用的,但还是忍不住加了一些奇怪的没用的知识进去,使得文章离自娱自乐更近了一步。 不过复习了一遭才发现自己确确实实忘记了不少基础的东西,得强迫自己以后多多学习了。
